Gelombang Transversal & Longitudinal

Gelombang Transversal

Gelombang transversal adalah gelombang yang arah getarnya tegak lurus dengan arah rambat gelombang. Bentuk gelombang transversal dapat dilihat melalui tali yang diikatkan pada sebuah tiang kemudian digerakkan. Tali tersebut akan membentuk lengkungan yang terdiri atas bukit dan lembah. Bagian gelombang yang melengkung ke atas disebut bukit. Sedangkan bagian gelombang yang melengkung ke bawah disebut lembah.

Pada gelombang transversal, panjang satu gelombang transversal dinyatakan dalam 1 (satu) bukit dan 1 (satu) lembah. Gambar panjang satu gelombang transversal yang terdiri dari satu bukit dan satu lembah dapat dilihat seperti berikut.

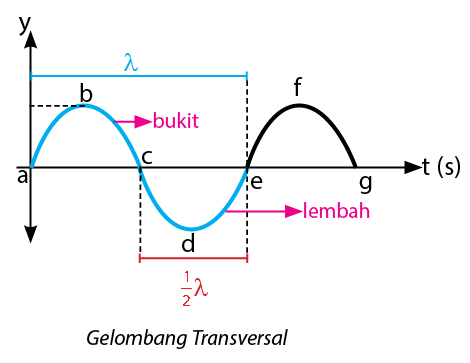
Karakteristik Gelombang Transversal:

Arah rambatanya tegak lurus terhadap arah getarannya.
Gelombang transversal berbentuk bukit dan lembah.

Contoh Gelombang Transversal:

Gelombang pada tali
Gelombang pada permukaan air
Gelombang cahaya

Gelombang Longitudinal

Gelombang longitudinal adalah gelombang yang arah getarnya berimpit/sejajar dengan arah rambat gelombang. Bentuk gelombang longitudinal dapat dilihat melalui sebuah slinki yang salah satu ujungnya diikatkan pada tiang. Slinki tersebut direntangkan dan disentakkan, sehingga akan terbentuk rapatan dan regangan pada slinki. Bagian slinki yang lebih renggang disebut regangan. Sedangkan bagian slinki yang lebih rapat disebut rapatan.

Pada gelombang longitudinal, panjang satu gelombang dinyatakan dalam 1 (satu) rapatan dan 1 (satu) regangan. Gambar panjang satu gelombang pada gelombang longitudinal yang terdiri atas satu rapatan dan satu regangan dapat dilihat pada gambar berikut.

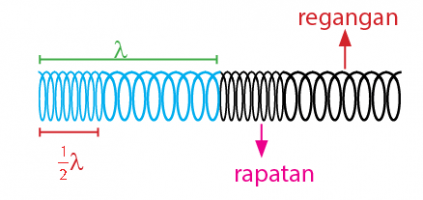
Karakteristik Gelombang Longitudinal:

Arah getar sejajar dengan arah rambatnya.
Gelombang logitudinal berbentuk rapatan dan regangan.

Contoh Gelombang Longitudinal:

Gelombang bunyi

Rumus pada Getaran dan Gelombang

Sekarang kita akan membahas rumus yang digunakan untuk menyelesaikan berbagai soal pada getaran dan gelombang. Rumus yang akan diberikan terkait periode (T), frekuensi (f), hubungan antara periode (T) dan frekuensi, dan cepat rambat gelombang (v). Simak rumus-rumus yang terdapat pada gelobang gelombang transversal dan gelombang longitudinal melalui pembahasan di bawah.

Periode (T)

Periode adalah waktu yang diperlukan untuk melakukan satu kali getaran. Persamaan Periode (T) dinyatakan sebagai perbandingan waktu dan banyaknya getaran yang dihasilkan.

Rumus periode (T) gelombang dinyatakan sebagai berikut.

$T = \frac{t}{n}$

Keterangan:

T = periode (s)

t = waktu (s)

n = banyaknya getaran

Frekuensi (f)

Frekuensi adalah banyaknya getaran yang terjadi selama 1 sekon. Rumus persamaan frekuensi (f) menyatakan perbandingan antara banyaknya getaran per satu satuan waktu. Persamaan frekuensi (f) memiliki hubungan kebalikan dengan persamaan periode (T).

Rumus frekuensi (f) gelombang dinyatakan sebagai berikut.

$f = \frac{n}{t}$

Keterangan:

f = frekuensi (Hz)

t = waktu (s)

n = banyaknya getaran

Hubungan antara frekuensi (f) dan periode (T)

Antara persamaan frekuensi (f) dan periode (T) memiliki hubungan kebalikan. Sehingga, antara kedua persamaan tersebut dapat dibentuk hubungan persamaan. Rumus hubungan persamaan frekuensi (f) dan periode (T) adalah sebagai berikut.

$f = \frac{1}{T} \; \textrm{atau} \; T = \frac{1}{f}$

Keterangan:

f = frekuensi (Hz)

T = periode (s)

Rumus Cepat Rambat Gelombang

Selain persamaan rumus frekuensi (f), rumus periode (T), serta hubungan antara frekuensi (f) dan Periode (T) yang telah dibahas di atas, terdapat pula persamaan yang menyatakan rumus cepat rambat gelombang. Persamaan dalam rumus cepat rambat gelombang menyatakan hubungan antara cepat rambat gelombang, periode (T)/frekuensi (f), dan panjang gelombang. Berikut ini adalah rumus yang dapat digunakan untuk mengetahui cepat rambat gelombang.

$v = \frac{\lambda}{T}$

atau

$v = \lambda \cdot f$

Keterangan:

v = cepat rambat gelombang (m/s)

$\lambda$ = panjang gelombang (m)

T = periode

Contoh Soal dan Pembahasan

1. Perhatikan gambar berikut!

Jika waktu yang dibutuhkan untuk menempuh jarak A ke B adalah 8 sekon, cepat rambat gelombang tersebut adalah ….

A. 2 m/s
B. 4 m/s
C. 6 m/s
D. 8 m/s

Pembahasan:

Perhatikan gambar di bawah!

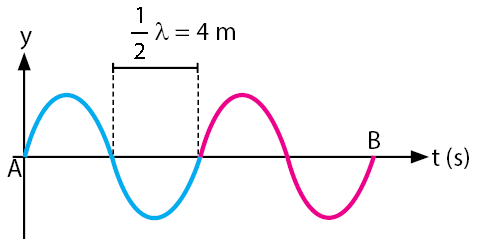
Diketahui:

$t_{AB} = 8 \; s$

$n = 2$

$\frac{1}{2} \lambda = 4 \; m \rightarrow \lambda = 8 \; m$

Ditanyakan:

$v = ... ?$

Jawab: Mencari nilai periode terlebih dahulu.

$T = \frac{t}{n}$

$T = \frac{8}{2}$

$T = 4 \; s$

Mencari cepat rambat gelombang:

$v = \frac{\lambda}{T}$

$v = \frac{8}{4} = 2 \; \frac{m}{s}$

Jawaban: A

2. Gelombang terbentuk dalam waktu 3 detik, maka frekuensi gelombangnya adalah ... .

a. 3 Hz d. 15 Hz

b. 5 Hz e. 30 Hz

c. 10 Hz

kunci jawaban: C

penyelesaian/pembahasan:

dengan rumus frekuensi gelombang

f = n/t = 30/3 = 10 Hz

3. Sebuah slinki menghasilkan gelombang longitudinal dengan jarak renggangan dan rapatan berurutan 7,5 cm. Jika cepat rambat gelombangnya sebesar 3 m/s, maka frekuensi gelombangnya sebesar ... .

a. 3 Hz d. 20 Hz

b. 7,5 Hz e. 22,5 Hz

c. 10 Hz

kunci jawaban: D

pembahasan/penyelesaian:

½ λ = 7,5 (λ = panjang 1 rapatan + 1 regangan)

λ = 15 cm =15.10^-2m

dengan rumus cepat rambat gelombang

v = λ . f

3 = 15.10^-2 . f

f = 300/15 = 20 Hz

4. Jarak antara dua buah titik yang berdekatan dengan fase sama adalah 8 cm. dan memiliki periode gelombang sebesar 2 sekon, maka besar cepat rambat gelombangnya adalah ... .

a. 2 cm/s d. 16 m/s

b. 4 cm/s e. 32 m/s

c. 8 cm/s

kunci jawaban:

pembahasan/penyelesaian:

Jarak antara dua buah titik yang berdekatan dengan fase sama = λ

Sehingga:

λ = 8 cm

T = 2 s

v = λ/T

v = 8/2 = 4 cm/s

5. Salah satu ujung seutas tali yang cukup panjang digetarkan sehingga timbul gelombang transversal. Jika jarak dua bukit berdekatan adalah 40 cm. Dan frekuensi sumber getaran sebesar 10 Hz, cepat rambat gelombang pada tali tersebut adalah . . . .

a. 4 m/s d. 0,4 m/s

b. 2 m/s e. 0,2 m/s

c. 1 m/s

kunci jawaban:

pembahasan/penyelesaian:

jarak dua bukit berdekatan adalah λ

λ = 40 cm = 0,4 m

f = 10 Hz

v = λ . f = 0,4 . 10 = 4Hz

Cari Blog Ini

Anak MIPA Berkarya