Lingkaran XI MIPA Semester 2
Persamaan umum lingkaran
Terdapat persamaan umum, seperti dibawah ini :
Dilihat dari persamaan diatas, dapat ditentukan titik pusat serta jari – jarinya, adalah :
Titik pusat lingkaran adalah :
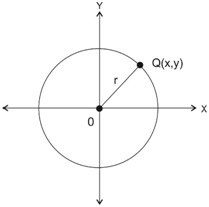
Pada pusat P (a,b) dan jari-jari r
Dari sebuah lingkaran jika diketahui titik pusat dan jari-jari nya, akan didapatkan yaitu dengan rumus :
Jika diketahui titik pusat suatu lingkaran dan jari – jari lingkaran dimana (a,b) adalah titik pusat dan r adalah jari-jari dari lingkaran.
Dari persamaan yang didapat diatas, kita dapat menentukan apakah termasuk titik terletak pada lingkaran tersebut, atau di dalam atau diluar. Untuk menentukan letak titik tersebut, yaitu dengan menggunakan subtitusi titik pada variabel x dan y lalu dibandingkan hasil nya dengan kuadrat dari jari-jari lingkaran.
Suatu titik M(x1, y1) terletak:
Pada lingkaran:
Di dalam lingkaran:
Di luar lingkaran:
Pada dengan pusat O (0,0) dan jari-jari r
Jika titik pusat di O(0,0), maka lakukanlah subtitusi pada bagian sebelum nya, yakni :
Dari persamaan diatas, maka, dapat ditentukan letak suatu titik terhadap lingkaran tersebut.
Suatu titik M(x1, y1) terletak:
Pada lingkaran:
Di dalam lingkaran:
Diluar lingkaran
Bentuk umum dari persamaannya dapat dinyatakan dalam beberapa bentuk berikut.
(x – a)2 + (y – b)2 = r2 , atau
X2 + y2 – 2ax – 2by + a2 + b2 – r2 = 0 , atau
X2 + y2 + Px + Qy + S = 0 , dengan P = -2a, Q = -2b, dan S = a2 + b2 – r2
Perpotongan Garis dan Lingkaran
Suatu lingkaran dengan persamaan x2 + y2 + Ax + By + C = 0 dapat ditentukan apakah suatu garis h dengan persamaan y = mx + n tersebut tidak menyentuh, menyinggung, atau memotongnya dengan menggunakan prinsip diskriminan.
……. (persamaan 1)
…….. (persamaan 2)
Dengan mensubtitusi persamaan 2 ke persamaan 1, akan diperoleh suatu bentuk persamaan kuadrat, yaitu:
Dari persamaan kuadrat diatas, dengan membandingkan nilai diskriminannya, dapat dilihat apakah garis tidak menyinggung/memotong, menyinggung atau memotong lingkaran.
Garis h tidak memotong/menyinggung lingkaran, maka D < 0
Garis h menyinggung lingkaran, maka D = 0
Garis h memotong lingkaran, maka D > 0
Persamaan Garis Singgung Lingkaran
1. Persamaan garis singgung melalui sebuah titik pada lingkaran
Garis singgung pada suatu lingkaran tepat bertemu dengan satu titik yang terletak pada lingkaran. Dari titik pertemuan dari garis singgung dan lingkaran, dapat ditentukan persamaan garis dari garis singgung tersebut.
Persamaan garis singgung lingkaran yang melalui titik P(x1, y1), dapat ditentukan yaitu:
- Bentuk
Persamaan garis singgungnya
- Bentuk
Persamaan garis singgungnya
- Bentuk
Persamaan garis singgungnya



















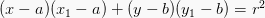


Komentar
Posting Komentar